Modern assistants like ChatGPT feel helpful because they’re not only trained to predict text, they’re trained to behave. The method behind this shift is reinforcement learning with human feedback (RLHF). In this article, we go step‑by‑step: the intuition, the 3‑stage pipeline (SFT → Reward Model → PPO), the math (Bradley–Terry, KL‑penalized objectives), NumPy/PyTorch code, diagrams, practical tips, safety concerns, and where RLHF sits among alternatives like DPO, RLAIF, and Constitutional AI.

---

1) Why Do We Need RLHF?

---

Plain English. Pretrained language models learn to continue text. That alone can produce factual, polite, or wild outputs—depending on the data. There is no explicit signal of what we want. RLHF adds that signal by letting humans rank outputs, then steering the model to prefer ranked‑higher answers.

Analogy. A student (the model) learns grammar by reading billions of sentences (pretraining), then learns “what’s appropriate” by receiving rubrics and feedback from instructors (human raters). The final exam uses the rubric (reward model) to grade answers and push the student toward desired behavior.

---

2) The 3‑Stage RLHF Pipeline

---

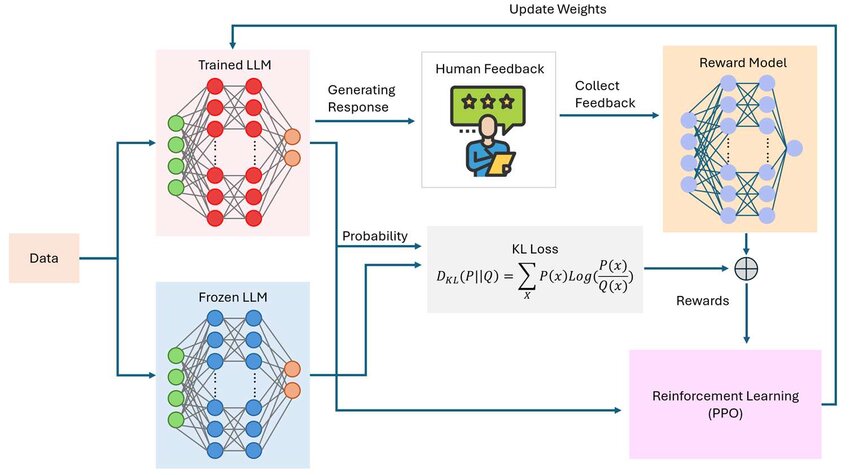
1. Supervised Fine‑Tuning (SFT): Make the model follow instructions using curated (prompt, response) pairs.
2. Reward Model (RM): Collect human pairwise preferences for multiple responses to the same prompt; train a model to score answers.
3. Policy Optimization: Treat the LM as a policy; optimize with RL to maximize the learned reward, while penalizing divergence from a reference model.

---

3) Stage 1 — Supervised Fine‑Tuning (SFT)

---

Goal. Teach basic instruction‑following. Start from a pretrained LM and fine‑tune on human‑written completions to prompts. This stabilizes later stages and sets a good “style”.

# Tiny SFT sketch (PyTorch + HF Transformers)
from transformers import AutoModelForCausalLM, AutoTokenizer
import torch

model_name = "gpt2"
tok = AutoTokenizer.from_pretrained(model_name)
model = AutoModelForCausalLM.from_pretrained(model_name)

example = {"prompt": "Explain gravity to a child:",
           "response": "Gravity is the invisible pull that makes things fall down to Earth."}

inp_ids = tok(example["prompt"], return_tensors="pt").input_ids
lbl_ids = tok(example["response"], return_tensors="pt").input_ids

out = model(input_ids=inp_ids, labels=lbl_ids)
print("SFT loss:", float(out.loss))

---

4) Stage 2 — Reward Model (Learning from Preferences)

---

Data. For each prompt \(x\), sample multiple model answers \(\{y_1,\dots,y_k\}\). Humans pick which answer is better (pairwise comparisons). We then train a model \(R_\phi(x,y)\) that scores answers so that preferred ones get higher scores.

Bradley–Terry model. For a pair \((y^+, y^-)\), the probability that \(y^+\) is preferred is \(\sigma \big(R(x,y^+) - R(x,y^-)\big)\), where \(\sigma\) is the logistic function.

# Minimal reward-model head on top of a base transformer (conceptual)
import torch, torch.nn as nn
from transformers import AutoModel

class RewardModel(nn.Module):
    def __init__(self, base_name="distilroberta-base"):
        super().__init__()
        self.base = AutoModel.from_pretrained(base_name)
        h = self.base.config.hidden_size
        self.value_head = nn.Linear(h, 1)

    def forward(self, input_ids, attention_mask=None):
        out = self.base(input_ids=input_ids, attention_mask=attention_mask)
        last_hidden = out.last_hidden_state  # [B, T, H]
        # simple: use last token; or use EOS positions / mean pool
        v = self.value_head(last_hidden[:, -1, :])  # [B, 1]
        return v.squeeze(-1)

Calibration tip. Keep reward magnitudes reasonable (e.g., z‑score rewards per batch). Extremely large/small rewards destabilize PPO.

---

5) Stage 3 — Policy Optimization (PPO + KL)

---

Goal. View the LM as a policy \(\pi_\theta(\cdot \mid x)\). Generate outputs, score them with the reward model \(R_\phi(x,y)\), and improve the policy using reinforcement learning. Use PPO for stable updates and add a KL penalty to keep the policy close to a reference model \(\pi_\text{ref}\) (often the SFT model).

PPO clip objective. With advantage \(\hat{A}_t\) and ratio \(r_t(\theta) = \frac{\pi_\theta(a_t|s_t)}{\pi_{\theta_\text{old}}(a_t|s_t)}\):

# (Concept) PPO loop sketch using trl library (Hugging Face)
# pip install trl accelerate datasets transformers
# from trl import PPOTrainer, PPOConfig

# config = PPOConfig(model_name="gpt2", learning_rate=1e-5, batch_size=8, target_kl=0.1)
# ppo_trainer = PPOTrainer(config, model, ref_model, tokenizer, reward_model)

# for batch_prompts in dataloader:
#     gen_texts = ppo_trainer.generate(batch_prompts, max_new_tokens=128)
#     rewards = reward_model.score(batch_prompts, gen_texts)  # your wrapper
#     stats = ppo_trainer.step(batch_prompts, gen_texts, rewards)

---

6) Math Corner: From Preferences to Policy

---

6.1 Bradley–Terry / Logistic preference

Train by maximizing the likelihood (equivalently minimizing the negative log‑likelihood in the section above).

6.2 Advantages and baselines

6.3 KL‑penalized RL objective

Interpret \(\beta\) as a “leash length”: higher means tighter to the reference model.

6.4 Tiny numeric example (PPO clip)

Suppose \(\hat{A}=+2\). If \(r=1.5\) and \(\epsilon=0.2\), then \(\text{clip}(r,0.8,1.2)=1.2\). The PPO term uses min\((1.5\cdot 2,\; 1.2\cdot 2) = 2.4\) (clipped). Clipping avoids huge risky jumps.

---

7) Hands‑On: Toy RLHF in Code

---

7.1 NumPy: simulate preferences & a tiny PPO‑ish step

import numpy as np

rng = np.random.default_rng(0)

# synthetic "true" score for responses: f(y) = - (y-3)^2 + 10 (peak at y=3)
def true_reward(y):
    return - (y - 3.0)**2 + 10.0

# policy: Gaussian over y with mean mu and fixed std
mu = 0.0
std = 1.0

def sample_response(mu, std, n=64):
    return rng.normal(mu, std, size=n)

def kl_gaussians(mu_new, mu_old, std=1.0):
    # KL(N(mu_new, std^2) || N(mu_old, std^2)) = ( (mu_old-mu_new)^2 )/(2*std^2)
    return ((mu_old - mu_new)**2) / (2*std**2)

beta = 0.1
lr = 0.05

for step in range(60):
    y = sample_response(mu, std, n=128)
    rewards = true_reward(y)

    # scalar objective: mean reward - beta*KL to a reference (here: mu_ref=0 for demo)
    mu_ref = 0.0
    kl = kl_gaussians(mu, mu_ref, std)
    J = rewards.mean() - beta * kl

    # simple gradient wrt mu: d/dmu E[r(y)] for Gaussian ≈ E[r'(y)] by score function approximations (toy)
    # here we cheat using finite diff on mu to keep it short:
    eps = 1e-3
    mu_plus = mu + eps
    y2 = sample_response(mu_plus, std, n=2000)
    grad_mu_reward = (true_reward(y2).mean() - rewards.mean()) / eps

    grad_mu_kl = - beta * ( (mu_ref - mu) / (std**2) )  # d/dmu [ - beta * KL ] term

    grad = grad_mu_reward + grad_mu_kl
    mu += lr * grad

    if step % 10 == 0:
        print(f"step {step:02d}  mu={mu:.3f}  J={J:.3f}  KL={kl:.4f}")

This toy shows how a KL penalty prevents the policy mean \(\mu\) from drifting too far from a reference, even as it chases higher reward.

7.2 PyTorch: training a reward model with synthetic pairs

import torch, torch.nn as nn, torch.optim as optim
import math

# Synthetic features for (x, y). We'll keep it 1D: y is the response scalar; x is ignored.
# Label pairs via true_reward as above; create (y_plus, y_minus) with preference y_plus > y_minus.

def true_reward_t(y):
    return - (y - 3.0)**2 + 10.0

class TinyRM(nn.Module):
    def __init__(self):
        super().__init__()
        self.net = nn.Sequential(nn.Linear(1, 32), nn.Tanh(), nn.Linear(32, 1))
    def forward(self, y):  # y: [B, 1]
        return self.net(y).squeeze(-1)  # [B]

rm = TinyRM()
opt = optim.Adam(rm.parameters(), lr=1e-3)
sigm = nn.Sigmoid()

for epoch in range(2000):
    y_plus  = torch.randn(256,1)*1.5 + 3.0  # around optimum
    y_minus = torch.randn(256,1)*1.5 + 0.0  # less optimal
    # enforce plus is really better (swap if needed)
    tp = true_reward_t(y_plus).squeeze(-1)
    tm = true_reward_t(y_minus).squeeze(-1)
    swap = (tm > tp).nonzero(as_tuple=True)[0]
    y_plus[swap], y_minus[swap] = y_minus[swap].clone(), y_plus[swap].clone()

    r_plus  = rm(y_plus)
    r_minus = rm(y_minus)
    logits = r_plus - r_minus
    loss = - torch.log(sigm(logits) + 1e-9).mean()

    opt.zero_grad()
    loss.backward()
    opt.step()

    if epoch % 400 == 0:
        with torch.no_grad():
            test = torch.linspace(-2, 8, 21).view(-1,1)
            rhat = rm(test)
        print(f"epoch {epoch}  loss={loss.item():.4f}  rhat@3≈{float(rhat[ test.squeeze()==3 ] if (test==3).any() else rhat[10]):.3f}")

---

8) Practical Guidelines (What Actually Matters)

---

• Data quality > everything. Clear rater instructions, examples of harmless refusal, factual grounding.
• Diversity of prompts. Include safety‑critical, multilingual, edge cases, and “jailbreak‑like” attempts.
• KL targeting. Start with moderate \(\beta\) (or target_kl≈0.05–0.2), monitor quality drift & perplexity.
• Reward shaping. Normalize per batch; inspect reward histograms; watch for collapse.
• Evaluation. Human eval on helpfulness/harmlessness/truthfulness; adversarial tests; toxicity & bias audits.
• No‑decay groups. If you use decoupled weight decay (AdamW), don’t decay layer norms/biases.

---

9) Case Studies (High‑Level)

---

• Instruction‑tuned LMs (e.g., Instruct‑style): SFT on human‑written answers → RM from preferences → PPO with KL → big jumps in helpfulness.
• Safety layers: Refusal training + harm policies; special prompts for safety‑first behavior.
• “Constitutional AI” (Anthropic‑style): Replace part of human feedback with a written constitution; the model critiques & revises itself to comply.

---

10) RLHF Alternatives & Cousins

---

10.1 DPO — Direct Preference Optimization

Optimizes policy directly from preferences without an explicit reward model or PPO rollouts. A common simplified loss (conceptually) uses logits from the current policy against a reference:

Pros: simpler pipeline; no PPO. Cons: different trade‑offs; relies on good reference and careful β/temperature choices.

10.2 RLAIF — Reinforcement Learning from AI Feedback

Use a strong “teacher” model to label preferences instead of humans. Scales cheaply, but risks transferring teacher biases.

10.3 Constitutional AI

Use principles (a “constitution”) to guide self‑critique and revision. Reduces human labor; works well for safety style constraints.

---

11) Beyond Chatbots: Where RLHF Shows Up

---

• Summarization: preferences for faithful, concise summaries vs. verbose/hallucinated ones.
• Search & ranking: pairwise ranking of results tuned to user satisfaction signals.
• Robotics: human preferences over trajectories (preference‑based RL).
• Vision‑language: choose better captions or step‑by‑step rationales.

---

12) Watch: A Clear RLHF Explainer

---

---

13) Mini‑Glossary

---

• RLHF — Reinforcement Learning with human feedback via preferences.
• SFT — Supervised Fine‑Tuning: instruction data to teach baseline behavior.
• Reward Model — Model that scores responses so preferred ones rank higher.
• PPO — Proximal Policy Optimization for stable policy updates.
• KL Penalty — Regularizer that keeps policy close to a reference model.
• DPO — Direct Preference Optimization; skip explicit RM/PPO.
• RLAIF — RL from AI feedback (model labels preferences).

---

14) References & Further Reading

---

1. Wikipedia: Reinforcement learning
2. Wikipedia: Bradley–Terry model
3. Wikipedia: Proximal Policy Optimization
4. Vaswani et al. (2017) — Attention is All You Need
5. Stiennon et al. (2020) — Learning to summarize with human feedback
6. Rafailov et al. (2023) — Direct Preference Optimization
7. Constitutional AI (overview)

---

15) FAQ

---

Q1. Is RLHF just “making models nice”?

No. It tunes behavior to align with human preferences for helpfulness, safety, and clarity. That includes saying “no” when a request is harmful.

Q2. Do I always need PPO?

No. Methods like DPO avoid PPO by directly optimizing the policy from preferences. PPO is popular, but not mandatory.

Q3. Why do we need a reference model for KL?

To prevent the policy from drifting into degenerate modes that exploit the reward model. The reference (often SFT) anchors language quality.

Q4. Can I use AI labelers instead of humans?

Yes (RLAIF), but you inherit teacher biases. Many pipelines mix human and AI feedback.

Q5. Is RLHF enough to solve “AI alignment”?

No. It’s a practical tool that helps, but it doesn’t guarantee perfect truthfulness/safety. Use layered defenses and continuous evaluation.