L2 Regularization (Ridge / Weight Decay) — A Beginner-Friendly Deep Dive
Overfitting is when a model memorizes noise instead of learning patterns. L2 regularization (ridge / weight decay) fixes a surprising amount of it with one idea: gently penalize large weights. In this guide we take it slow: a kid-level analogy, tiny numeric examples, the exact math, the geometry, the Bayesian story, how to pick λ, and working Python code in numpy, scikit-learn, and PyTorch.
1) Why do we need L2?

Plain English. Overfitting = great on training, poor on new data. It happens when the model uses very large, twitchy weights to chase noise.
Fix. Add a small penalty for large weights; the model still fits the data, but prefers simpler settings unless data begs otherwise.
2) What L2 regularization actually is
We add the squared size of the weights to the loss. A common definition (nice for gradients) is with a 1/2 factor:
- \(\lambda \gt 0\) controls the strength of the pull toward zero.
- We typically do not regularize the bias/intercept term.
- For classification (e.g., logistic regression), it’s the same idea—add \(\frac{\lambda}{2}\|w\|^2\) to the data loss.
3) From OLS to Ridge: the step-by-step math
Ordinary Least Squares (OLS). With design matrix \(X\in\mathbb{R}^{n\times p}\) and targets \(\mathbf{y}\in\mathbb{R}^n\):
Ridge (OLS + L2). Add \(\frac{\lambda}{2}\|\mathbf{w}\|^2\):
Setting the gradient to zero gives the closed form:
If you define OLS without the \(1/n\), the formula becomes \((X^\top X+\lambda I)^{-1}X^\top y\). Both are common; we’ll keep the \(n\lambda\) version consistent with the \(1/(2n)\) normalization above.
4) Gradient update & “weight decay” (why the weights shrink)
Gradient descent with learning rate \(\eta\) on \(\mathcal{L}_\lambda\) gives:
Key effect. Every step multiplies \(\mathbf{w}\) by \((1-\eta\lambda)\). That’s why L2 in optimizers is often called weight decay.
w ← w − η·(∇data) − η·wd·w where wd is the weight decay value (like λ).
5) Geometry: ellipse meets circle (why solutions get “rounded”)
OLS loss contours are ellipses in weight space; the L2 constraint \(\|\mathbf{w}\|^2\le c\) is a circle (sphere in higher-D). The optimum is where the smallest ellipse first touches the circle—tangency.
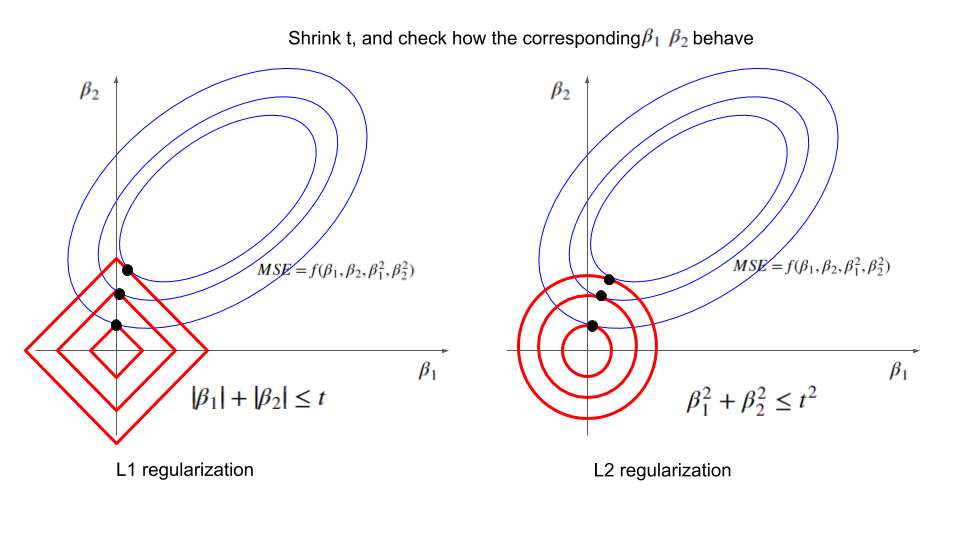
L2 vs L1. L1 is a diamond and loves corners → exact zeros (sparsity). L2 is a circle and shrinks everything smoothly (rarely exact zero).
6) Bayesian view: Gaussian prior ⇒ ridge
Assume noise \( \varepsilon\sim\mathcal{N}(0,\sigma^2I) \) and a prior \( \mathbf{w}\sim\mathcal{N}(\mathbf{0},\tau^2 I) \). Maximizing the posterior (MAP) yields ridge with \( \lambda=\sigma^2/\tau^2 \):
Interpretation. Larger noise \(\sigma^2\) or stronger belief that weights are small (small \(\tau^2\)) → bigger \(\lambda\).
7) SVD shrinkage: how ridge dampens weak directions
Let \(X=U\Sigma V^\top\) with singular values \(\sigma_1\ge\dots\ge\sigma_r\). In this basis, ridge scales components by:
Small \(\sigma_j\) (ill-conditioned directions) get shrunk most → better stability and less overfitting.
8) Choosing λ (practical and painless)
| Method | How | Good starting point |
|---|---|---|
| Cross-validation | Scan λ on a log grid; pick best validation score | \(10^{-4}\) … \(10^{1}\) |
| RidgeCV | Built-in scikit-learn cross-validated ridge | Decades grid, e.g., [1e-4, …, 10] |
| Empirical Bayes | Maximize marginal likelihood (advanced) | Use when you know noise priors |
9) Tiny numeric examples (feel the effect)
10) Hands-on (scikit-learn): overfit polynomial vs ridge/RidgeCV
import numpy as np, matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler, PolynomialFeatures
from sklearn.linear_model import LinearRegression, Ridge, RidgeCV
from sklearn.pipeline import make_pipeline
# 1) Data: noisy sine
rng = np.random.default_rng(42)
X = np.linspace(0, 10, 80)[:, None]
y = np.sin(X).ravel() + 0.5 * rng.normal(size=80)
# 2) Overfit baseline: degree-15 OLS (no regularization)
ols = make_pipeline(StandardScaler(with_mean=False), # keep bias out; poly adds bias if include_bias=True
PolynomialFeatures(15, include_bias=False),
LinearRegression())
ols.fit(X, y)
# 3) Ridge with a fixed alpha
ridge = make_pipeline(PolynomialFeatures(15, include_bias=False),
StandardScaler(), # scale features -> crucial
Ridge(alpha=10.0, fit_intercept=True, random_state=0))
ridge.fit(X, y)
# 4) RidgeCV to pick alpha automatically (across decades)
alphas = np.logspace(-4, 1, 20)
ridgecv = make_pipeline(PolynomialFeatures(15, include_bias=False),
StandardScaler(),
RidgeCV(alphas=alphas, store_cv_values=False))
ridgecv.fit(X, y)
print("Best alpha from CV:", ridgecv.named_steps['ridgecv'].alpha_)
# 5) Plot
Xp = np.linspace(0, 10, 400)[:, None]
plt.figure(figsize=(8,4))
plt.scatter(X, y, s=15, c='k', label='data')
plt.plot(Xp, ols.predict(Xp), 'r--', label='deg-15 OLS (overfit)')
plt.plot(Xp, ridge.predict(Xp), 'b-', label='deg-15 Ridge (α=10)')
plt.plot(Xp, ridgecv.predict(Xp),'g-', label='RidgeCV (best α)')
plt.legend(); plt.tight_layout(); plt.show()What to look for. OLS wiggles between points; Ridge yields a smoother curve; RidgeCV often lands on a value similar to what you’d choose by eye.
11) Hands-on (PyTorch): weight decay with proper parameter groups
import torch, torch.nn as nn
torch.manual_seed(0)
# Simple dataset: y = 2x + noise
N = 256
x = torch.linspace(-3, 3, N).unsqueeze(1)
y = 2*x + 0.7*torch.randn_like(x)
# Tiny model
model = nn.Sequential(nn.Linear(1, 32), nn.ReLU(), nn.Linear(32, 1))
# Parameter groups: decay weights, DON'T decay biases or norms
decay, no_decay = [], []
for name, p in model.named_parameters():
if p.requires_grad:
if name.endswith(".bias"):
no_decay.append(p)
else:
decay.append(p)
optim = torch.optim.AdamW([
{'params': decay, 'weight_decay': 1e-2},
{'params': no_decay, 'weight_decay': 0.0}
], lr=1e-3)
loss_fn = nn.MSELoss()
for step in range(2000):
optim.zero_grad()
pred = model(x)
loss = loss_fn(pred, y)
loss.backward()
optim.step()
if step % 400 == 0:
print(f"step {step:4d} loss={loss.item():.4f}")Why groups? Decaying biases/LayerNorm often hurts performance. Most training recipes decay only the “real capacity” weights (linear/conv kernels).
12) Common pitfalls & quick fixes
- Not scaling features. Fix:
StandardScaler()before ridge. - Regularizing the bias. Fix: exclude bias/intercept from L2.
- Too big λ → underfit. Training and validation both poor; reduce λ.
- Too small λ → overfit. Training great, validation poor; increase λ.
- Using Adam instead of AdamW. Prefer AdamW to decouple weight decay.
13) Watch: StatQuest on Ridge
14) Mini-Glossary
- Regularization — discourage overly complex models to improve generalization.
- L2 / Ridge — penalize squared weights; smooth shrinkage.
- L1 / Lasso — penalize absolute weights; encourages exact zeros.
- Weight decay — the optimizer form of L2: multiply weights by (1 − ηλ) each step (plus gradient).
- Bias–variance — small extra bias can reduce variance a lot → better test error.
15) References & Further Reading
- Hoerl & Kennard (1970). Ridge Regression: Biased Estimation for Nonorthogonal Problems. Technometrics.
- Hastie, Tibshirani, Friedman (2009). The Elements of Statistical Learning, Ch. 3 & 7.
- Bishop (2006). Pattern Recognition and Machine Learning, Ch. 3 & 7.
- Loshchilov & Hutter (2019). Decoupled Weight Decay Regularization (AdamW).
- Wikipedia: Ridge regression, Tikhonov regularization, Bias–variance trade-off.
16) FAQ
Q1. Should I use L2 for classification (logistic regression)?
Yes. Add \(\frac{\lambda}{2}\|w\|^2\) to the logistic loss. It improves stability and generalization.
Q2. Do I regularize the bias?
Usually no. In scikit-learn, that’s handled automatically; in PyTorch, exclude bias/LayerNorm from weight decay via parameter groups (see code above).
Q3. Is L2 better than L1?
Different goals. L2 = stability and smooth shrinkage (keeps most features). L1 = sparsity (feature selection). Elastic Net mixes both.
Q4. How large should λ be?
Start with cross-validation over decades (\(10^{-4}\) … \(10^{1}\)), standardize features, and let RidgeCV pick the winner.
Comments