Self-attention is the Transformer’s secret: each token decides which other tokens matter, and by how much. In this gentle guide, we build your intuition first, then show the math, shapes, and a tiny numerical walk-through. We’ll cover scaled dot-product attention, masking, multi-head attention, positional encoding, encoder vs decoder vs cross-attention, complexity, and practical PyTorch/NumPy code you can run.

1) Intuition: why attention?

In language, each word’s meaning depends on context. In “The bank will not loan money,” the word “bank” relates to finance; in “The boat reached the bank,” it relates to a river. Self-attention lets each token ask the others, “Are you relevant to me?” and then blend information accordingly.

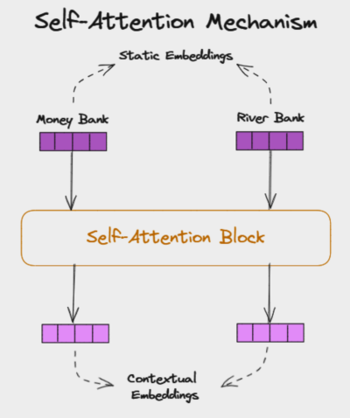
Unlike RNNs (sequential) or CNNs (local), attention compares every token with every other token in parallel, which is powerful—but also quadratic in sequence length.

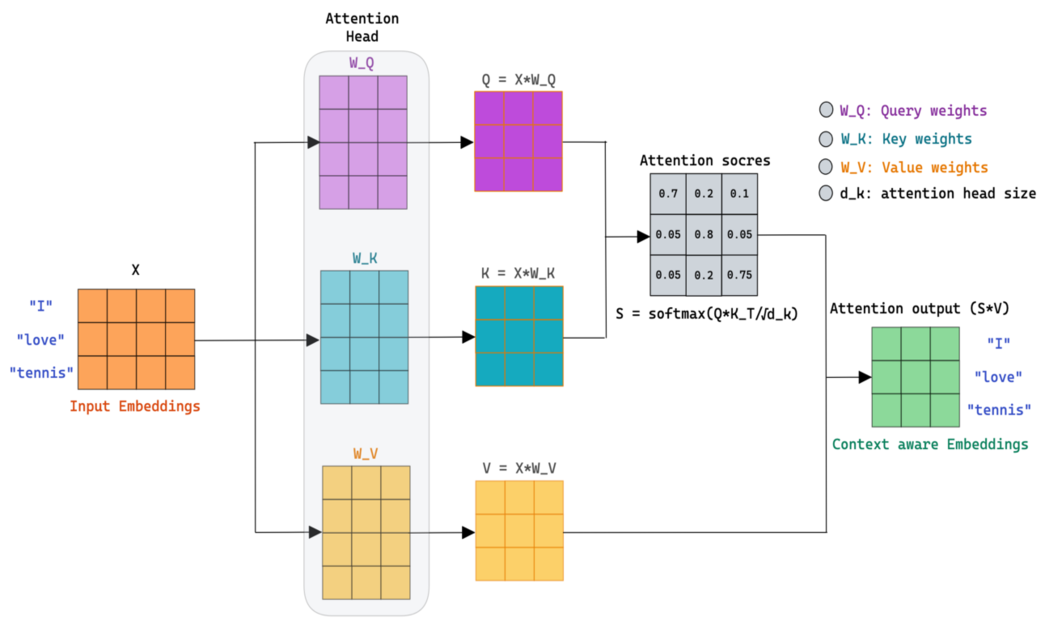
2) Queries, Keys, Values (Q/K/V)

Start with token embeddings \(X\in\mathbb{R}^{n\times d_\text{model}}\) (n = tokens). We learn three projections:

with \(W_Q,W_K,W_V\in\mathbb{R}^{d_\text{model}\times d_k}\) (often \(d_k=d_v=d_\text{model}/h\) for h heads). Intuition:

• Query: what a token is looking for.
• Key: what a token offers.
• Value: the actual information to pass along.

Shapes — If \(X\) is [n, d_model], and we use one head with \(d_k\), then \(Q,K,V\) are [n, d_k].

3) Scaled Dot-Product Attention

Scores are dot products between queries and keys. We scale by \(\sqrt{d_k}\) to keep gradients stable and apply softmax row-wise:

The matrix \(A\in\mathbb{R}^{n\times n}\) holds how strongly each token attends to each other token. Each row sums to 1.

4) Tiny numeric example (3 tokens, 2-D head)

This small arithmetic is worth doing once by hand; it makes the abstraction “click.”

5) Masking: causal (decoder) & padding (batching)

Causal mask (used in decoders / autoregressive models like GPT): token \(t\) cannot look ahead to \(t+1,\dots\). We add \(-\infty\) to forbidden logits before softmax.

Padding mask: When batching sequences of different lengths, pad with zeros and mask those positions so they receive and send no attention.

6) Multi-Head Attention (why more than one head?)

One head learns one notion of “relevance.” Multiple heads let the model attend to different patterns (syntax, coreference, long-range dependencies) simultaneously. Each head has its own \(W_Q,W_K,W_V\), smaller per-head dimension \(d_k\), and outputs are concatenated then projected:

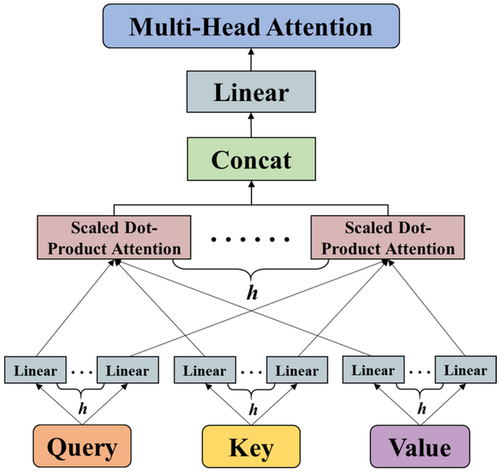
Shapes — With h heads and model dim d_model, we often set d_k = d_model / h. Each head: [n, d_k] → concat: [n, h*d_k]=[n, d_model].

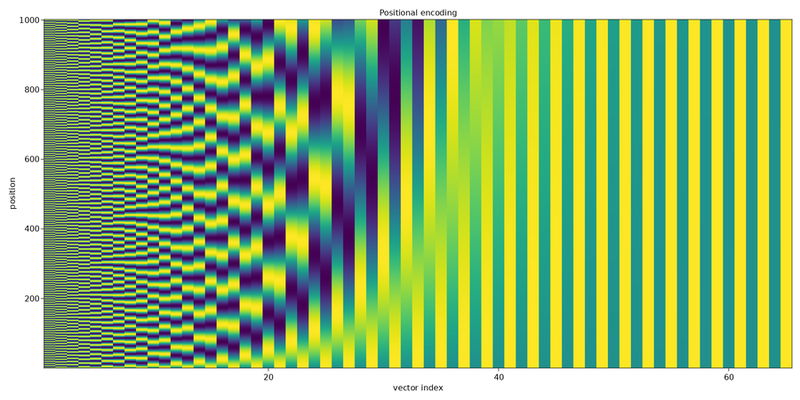
7) Positional Encoding (order matters!)

Self-attention has no sense of order by itself. We add positional encodings to token embeddings so the model knows token positions.

These sinusoids let the model infer relative positions. Many variants exist (learned, rotary, ALiBi, etc.), but sinusoidal remains a clear starting point.

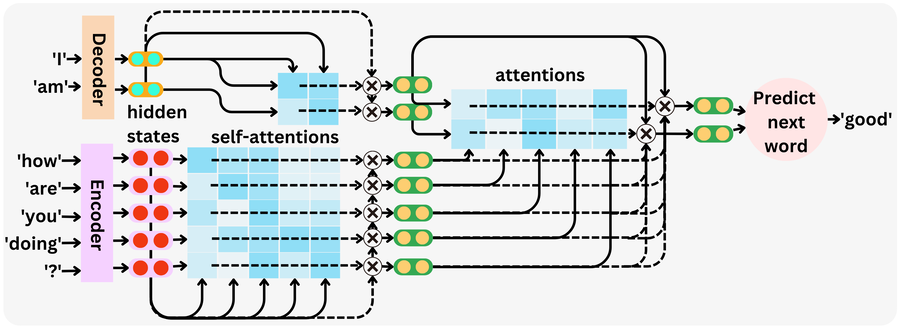
8) Encoder, Decoder & Cross-Attention (where self-attention lives)

• Encoder block (BERT-style): self-attention (bidirectional) + feed-forward, with residual connections and LayerNorm.
• Decoder block (GPT-style): masked self-attention (causal) + feed-forward. It looks only leftward in time.
• Cross-attention (encoder-decoder, e.g., translation): decoder queries attend over encoder keys/values: \(Q\) from decoder, \(K,V\) from encoder.

9) Complexity & efficiency

Computing \(QK^\top\) is \(O(n^2 d_k)\) time and \(O(n^2)\) memory for the attention matrix \(A\). That’s why long contexts are expensive. Practical tricks include:

• Chunking/windowed attention: restrict attention to local blocks.
• Linear/projection methods: approximate the softmax kernel to get near-linear time.
• Memory-efficient kernels: fuse operations and avoid storing full \(A\).

For beginners: start with the standard implementation; move to efficient variants only when you hit memory/time limits.

10) NumPy: self-attention in ~30 lines (with optional mask)

import numpy as np

def softmax(x, axis=-1):
    x = x - x.max(axis=axis, keepdims=True)
    e = np.exp(x)
    return e / e.sum(axis=axis, keepdims=True)

def self_attention_numpy(X, Wq, Wk, Wv, mask=None):
    """
    X:  [n, d_model]
    W*: [d_model, d_k]
    mask: [n, n] with 0 for allowed, -inf for blocked (added before softmax)
    """
    Q = X @ Wq   # [n, d_k]
    K = X @ Wk   # [n, d_k]
    V = X @ Wv   # [n, d_k] (or d_v)

    scores = (Q @ K.T) / np.sqrt(K.shape[1])  # [n, n]
    if mask is not None:
        scores = scores + mask                # add -inf to illegal connections

    A = softmax(scores, axis=-1)              # attention weights
    Y = A @ V                                 # [n, d_k]
    return Y, A

# Example
np.random.seed(0)
n, d_model, d_k = 5, 16, 8
X  = np.random.randn(n, d_model)
Wq = np.random.randn(d_model, d_k)
Wk = np.random.randn(d_model, d_k)
Wv = np.random.randn(d_model, d_k)

# causal mask (upper-triangular set to -inf)
mask = np.triu(np.ones((n,n)) * -1e9, k=1)
Y, A = self_attention_numpy(X, Wq, Wk, Wv, mask=mask)
print("Output shape:", Y.shape, "  Attn shape:", A.shape)

Notice the mask shape matches the \(n\times n\) attention score matrix.

11) PyTorch: from scratch and with MultiheadAttention

import torch, torch.nn as nn, math
torch.manual_seed(0)

def scaled_dot_product_attention(Q, K, V, attn_mask=None):
    # Q,K,V: [B, h, n, d_k]
    scores = Q @ K.transpose(-2, -1) / math.sqrt(Q.size(-1))  # [B,h,n,n]
    if attn_mask is not None:
        scores = scores + attn_mask                           # add -inf where blocked
    A = torch.softmax(scores, dim=-1)
    Y = A @ V                                                 # [B,h,n,d_k]
    return Y, A

class MultiHeadSelfAttention(nn.Module):
    def __init__(self, d_model=128, num_heads=4):
        super().__init__()
        assert d_model % num_heads == 0
        self.h = num_heads
        self.d_k = d_model // num_heads
        self.Wq = nn.Linear(d_model, d_model, bias=False)
        self.Wk = nn.Linear(d_model, d_model, bias=False)
        self.Wv = nn.Linear(d_model, d_model, bias=False)
        self.Wo = nn.Linear(d_model, d_model, bias=False)

    def forward(self, X, attn_mask=None):
        B, n, d_model = X.shape
        Q = self.Wq(X).view(B, n, self.h, self.d_k).transpose(1, 2)  # [B,h,n,d_k]
        K = self.Wk(X).view(B, n, self.h, self.d_k).transpose(1, 2)
        V = self.Wv(X).view(B, n, self.h, self.d_k).transpose(1, 2)

        Y, A = scaled_dot_product_attention(Q, K, V, attn_mask=attn_mask)  # [B,h,n,d_k],[B,h,n,n]
        Y = Y.transpose(1, 2).contiguous().view(B, n, self.h*self.d_k)     # concat heads
        out = self.Wo(Y)                                                   # [B,n,d_model]
        return out, A

# Example usage
B, n, d_model, h = 2, 6, 128, 4
X = torch.randn(B, n, d_model)

# causal mask: [1,1,n,n] broadcastable to [B,h,n,n]
mask = torch.triu(torch.ones(n, n)*-1e9, diagonal=1).unsqueeze(0).unsqueeze(0)
mha = MultiHeadSelfAttention(d_model=d_model, num_heads=h)
Y, A = mha(X, attn_mask=mask)
print(Y.shape, A.shape)  # torch.Size([2, 6, 128]) torch.Size([2, 4, 6, 6])

Built-in layer. PyTorch also offers nn.MultiheadAttention (note its default input shape is [seq_len, batch, embed_dim]):

mha = nn.MultiheadAttention(embed_dim=d_model, num_heads=h, batch_first=True)
# For self-attention, Q=K=V=X
causal_mask = torch.triu(torch.ones(n, n)*float('-inf'), diagonal=1)  # [n,n]
Y, A = mha(X, X, X, attn_mask=causal_mask)  # Y: [B,n,d_model], A: [B,h,n,n] (as of recent versions)

12) Visualizing attention (what heads learn)

Plot \(A\) as a heatmap: rows = query positions, columns = key positions. Different heads often specialize:

• Short-range syntax (e.g., adjective → noun)
• Long-range dependencies (e.g., subject ↔ verb)
• Coreference (e.g., “it” ↔ its referent)

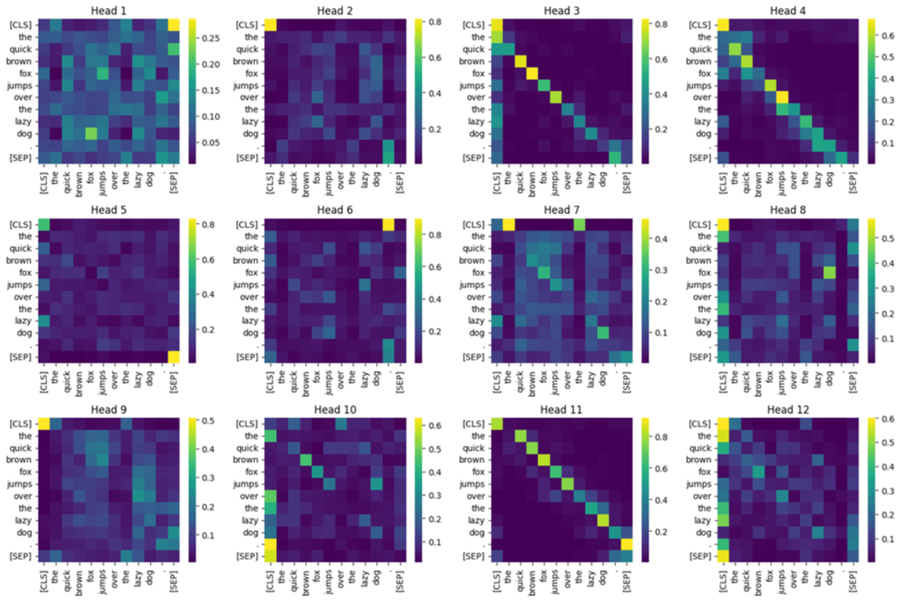
Not every head is interpretable; that’s normal. Use these plots for debugging intuition, not as a definitive explanation.

13) Mini-Glossary

• Self-attention — attention where \(Q,K,V\) all come from the same sequence.
• Cross-attention — \(Q\) from the decoder, \(K,V\) from the encoder.
• Scaled dot-product — use \(\frac{QK^\top}{\sqrt{d_k}}\) before softmax to stabilize training.
• Head — one attention subspace with its own \(W_Q,W_K,W_V\).
• Positional encoding — inject order info (sinusoidal or learned).
• Causal mask — prevents looking at future tokens in generation.

14) References & Further Reading

1. Vaswani, A. et al. (2017). Attention Is All You Need. NIPS. (Transformer overview)
2. Jay Alammar. The Illustrated Transformer. (Great visual blog)
3. Bengio, Goodfellow, Courville. Deep Learning — sequence models & attention.
4. Wikipedia: Attention (ML), Softmax, LayerNorm, Positional encoding.

15) Video: Karpathy — “Let’s build GPT from scratch”

16) FAQ

Q1. Why the \(\sqrt{d_k}\) scaling?

Dot products grow with \(d_k\). Scaling keeps logits in a good range so softmax isn’t overly peaky, stabilizing gradients.

Q2. What’s the difference between encoder self-attention and decoder self-attention?

Encoders attend bidirectionally (see all tokens). Decoders use a causal mask to prevent peeking at future tokens during generation.

Q3. Do I need multi-head attention?

Almost always yes. Multiple heads let the model capture different relationships in parallel; single-head is a useful teaching simplification.

Q4. How do positional encodings get added?

Typically by addition: \(X_\text{input}=X_\text{embed}+\text{PE}\). Learned or sinusoidal both work; sinusoidal gives nice extrapolation properties.

Q5. Why are long contexts expensive?

The attention matrix is \(n\times n\). Both compute and memory grow quadratically with sequence length.